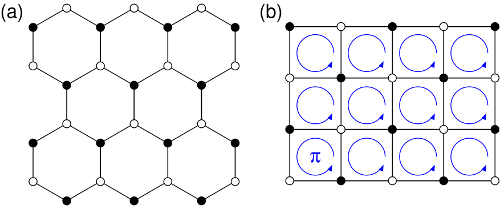
11 Marzo 2020 - www.pellegrinoconte.com

Cosa è un elettrone di Dirac?

Si tratta di un elettrone che è descritto dall’equazione di Dirac (Figura 1).

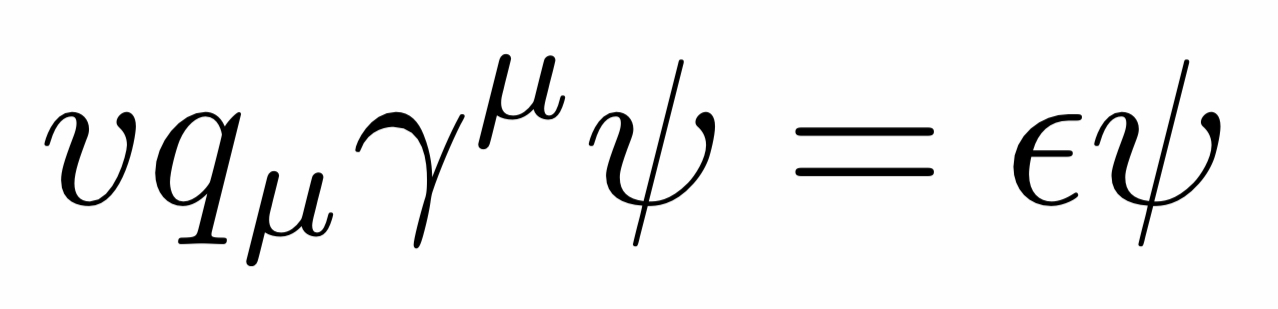
Semplice vero? Certo come no! Questa è la classica spiegazione a ciambella, ovvero un giro di parole che non spiega nulla se non si è un addetto ai lavori.

Cerchiamo di capire cos’è e perché è importante l’equazione di Dirac.

Ormai è noto a tutti che l’inizio del XX secolo è stato molto prolifico in termini scientifici. È nata, infatti, la meccanica quantistica (MQ) grazie alla quale oggi tutti hanno sentito parlare almeno una volta nella vita dell’equazione di Schoeredinger che, tra le tante cose, permette di descrivere il comportamento degli elettroni.

Una delle cose che viene insegnata a livello semplicistico a tutti gli studenti dei primi anni di corsi di studio scientifici è che l’equazione di Schoeredinger permette di definire gli orbitali come quella zona di spazio in cui esiste una buona probabilità di trovare gli elettroni. Come ho già scritto, questa è una supersemplificazione. Tuttavia fatemela passare per buona perché qui non si sta facendo una lezione di meccanica quantistica, bensì si cerca di fare un po’ di divulgazione per avvicinare concetti complessi a chi non è del settore.

Negli stessi anni in cui nasceva e si sviluppava la MQ, nasceva e si sviluppava anche la teoria della relatività ristretta (RR) di Albert Einstein. Questa si basa sostanzialmente su due postulati. Il primo postulato stabilisce che le leggi della fisica sono le stesse in tutti i sistemi di riferimento inerziali, il secondo afferma che la luce si propaga nel vuoto ad una velocità ben definita pari a 2.99 x 10⁸ m s^-1.

”Bene. Bravo. Ed ora? Dove vuoi arrivare mettendo assieme MQ e RR?” vi starete chiedendo.

Abbiate un attimo di pazienza, per favore. Lasciatemi ancora poche parole per arrivare al punto.

Meccanica quantistica e relatività ristretta sono due facce della stessa medaglia.

Fin da quando le due teorie, della MQ e della RR, si sono affermate, gli studiosi hanno cercato di unificarle. Tuttavia, tra le tante difficoltà che essi hanno incontrato, una particolarmente “ostica” è stata quella relativa alla asimmetria tra spazio e tempo della teoria di Schoeredinger che mal si conciliava con la simmetria spazio-temporale di Einstein. In altre parole, mentre Schoeredinger trattava spazio e tempo come se fossero due cose distinte e separate, Einstein considerava le dimensioni spaziali alla stessa stregua della dimensione temporale (prego i miei amici fisici di non essere troppo severi con me se sto semplificando troppo. Anzi, vi invito a correggermi se ritenete che io stia andando fuori dal seminato).

Solo Dirac, grazie alla sua genialità, riuscì a risolvere il problema elaborando una equazione (quella dell’immagine di Figura 1) con la quale riuscì a trattare le particelle quantistiche (quindi anche gli elettroni) nel regime relativistico.

Ma allora, a cosa serve sapere cosa sono gli elettroni di Dirac?

L’equazione di Dirac descrive molto bene il comportamento degli elettroni nei semiconduttori ed in sistemi quali il grafene. Per associazione, anche se studi del genere non sono stati ancora condotti, l’equazione di Dirac dovrebbe descrivere bene anche il comportamento di sistemi simil-grafene quali il biochar. Tuttavia, bisogna aggiungere che il numero di tecniche analitiche capaci di confermare sperimentalmente il comportamento degli elettroni secondo Dirac si può contare sulla punta delle dita di una sola mano. Si tratta di tecniche che sono “maneggiate” con una certa familiarità dai fisici, ma che per un chimico sono alquanto “ostiche”.

La risonanza magnetica nucleare (NMR) e gli elettroni di Dirac.

È di pochi giorni fa la notizia che su Nature Communication è apparso uno studio attraverso cui, per la prima volta, sono stati osservati mediante NMR (una tecnica molto amata dai chimici, incluso me che faccio l’NMR-ista sin dal 1992) gli effetti che gli stati elettronici di Dirac (ovvero quelli descritti dall’equazione di Figura 1) hanno sul comportamento dei nuclei di una lega metallica fatta da Bismuto e Tellurio (Bi₂Te₃) che viene utilizzata come isolante.
Se avete voglia di leggere l’articolo originale basta cliccare sull’immagine qui sotto.

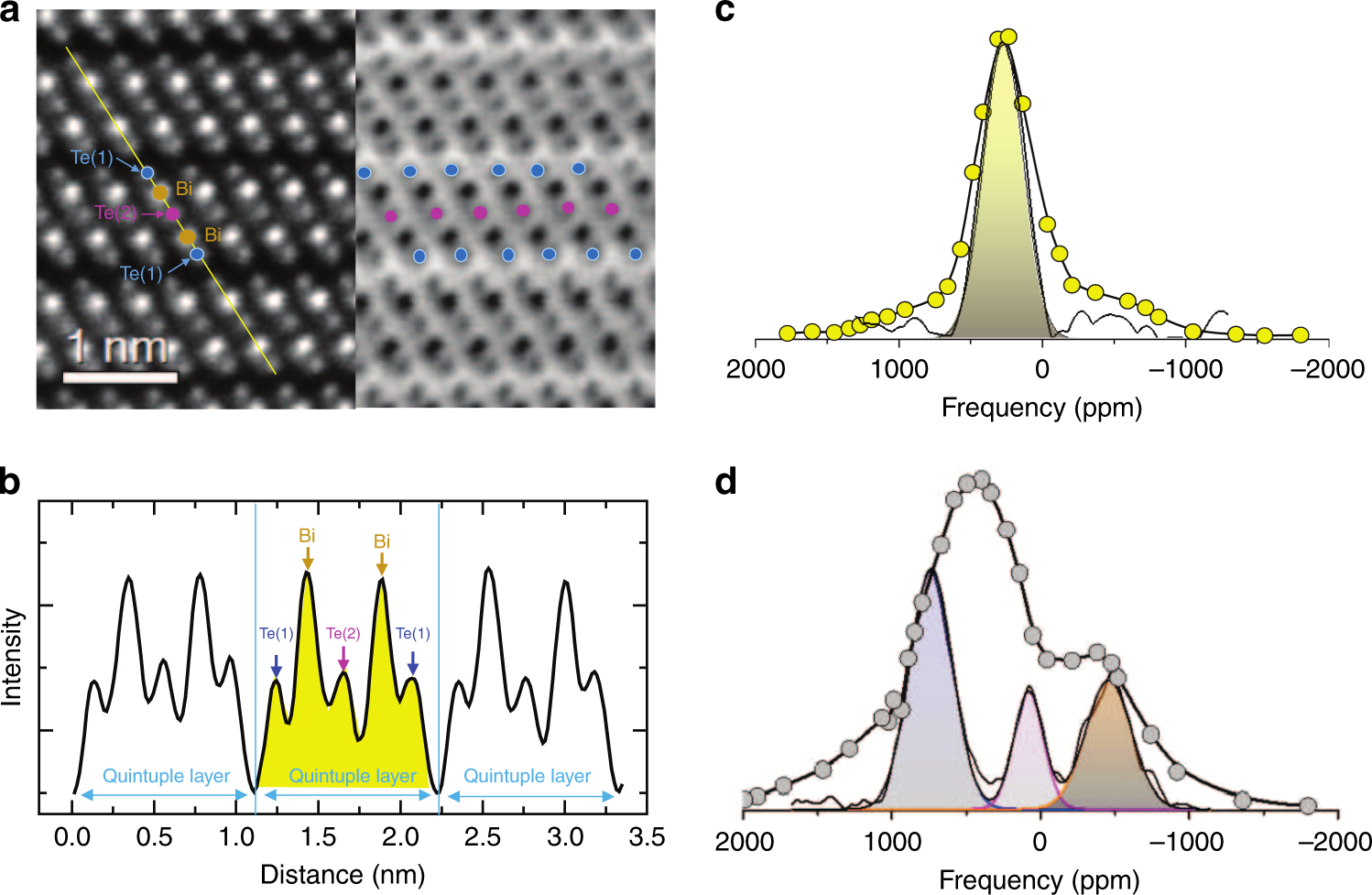
**Figura 2.** Immagine tratta dall’articolo di Nature Communications.

Ed allora?

Bella domanda. Intanto si aggiunge una nuova tecnica a quelle già usate per lo studio del comportamento degli elettroni e la verifica sperimentale dell’equazione di Dirac. Inoltre, si aprono nuovi scenari per la progettazione di nuovi materiali con proprietà sempre più sofisticate da poter utilizzare nei campi più disparati come la ricerca spaziale o quella medica.